🎈前言

AVL 树就是平衡二叉搜索树。它的节点左右子树高度相差不超过 1，当超过 1 时，它通过左旋和右旋操作降低树高，保持这一性质，降低平均搜索长度。对 AVL 树而言，插入、查找、删除节点的时间复杂度都能维持在 O(logn)，适用于处理有序的结构中的增删改查操作。

最近发现自己在做 Leetcode 的时候有点吃力，然后就闲来没事复习一下算法和数据结构，恰好在学 rust，这里我就用 rust 来实现一个 AVL 树。感觉用 rust 实现的难度主要在于它复杂的借用和所有权规则了，不过我也不太懂，这里就不多涉及了，把 AVL 树写出来就完事了。

说起来这种有序表的题目其实在 Leetcode 也挺少见的，这里找了个少见的例子，406 根据身高重建队列，虽然不用平衡树之类的解法在 $O(n^2)$ 复杂度下也能通过就是了。这是我的题解。

🎇类型定义

除了基础的 AVL 树外，我希望实现一个 AVL 树，可以实现排名、节点前驱后继等进一步的 $O(logn)$ 时间复杂度（$n$ 是树中节点个数）的查询。这样子就需要记录重复值个数count和子树大小size。不妨认为没有子树的单独一个节点树高为 1。我们先来定义一下类型，使用Box记录树的节点：

rust
#[derive(Debug)]
struct AVLTreeNode {
    key: i32,
    height: i32,
    size: i32,
    count: i32,
    left: OptionBoxAVLTreeNode,
    right: OptionBoxAVLTreeNode,
}
type BoxAVLTreeNode = Box<AVLTreeNode>;
type OptionBoxAVLTreeNode = Option<
    BoxAVLTreeNode
>;
struct AVLTree {
    root: OptionBoxAVLTreeNode,
}

实现new和属性获取的方法：

rust
impl AVLTreeNode {
    fn new(key: i32) -> Box<Self> {
        Box::new(Self {
            key,
            height: 1,
            size: 1,
            count: 1,
            left: None,
            right: None
        })
    }
}
impl AVLTree {
    fn new() -> Self {
        AVLTree { root: None }
    }
    fn size(node: &OptionBoxAVLTreeNode) -> i32 {
        match node {
            Some(node) => node.size,
            None => 0,
        }
    }
    fn count(node: &OptionBoxAVLTreeNode) -> i32 {
        match node {
            Some(node) => node.count,
            None => 0,
        }
    }
    fn height(node: &OptionBoxAVLTreeNode) -> i32 {
        match node {
            Some(node) => node.height,
            None => 0,
        }
    }
    fn key(node: &OptionBoxAVLTreeNode) -> Option<i32> {
        match node {
            Some(node) => Some(node.key),
            None => None,
        }
    }
}

🎆节点更新

当插入、删除、旋转操作发生后，节点或者其子节点发生变化时，需要递归向上更新节点的height、size、count这些值，定义一个update函数。节点的height为子树height最大值 + 1，size为子树size之和再加上自身的数量count。

rust
fn update(node: &mut BoxAVLTreeNode) {
    let left_height = Self::height(&node.left);
    let right_height = Self::height(&node.right);
    let left_size = Self::size(&node.left);
    let right_size = Self::size(&node.right);
    let self_count = node.count;
    
    node.height = std::cmp::max(left_height, right_height) + 1;
    node.size = left_size + right_size + self_count;
}

✨旋转操作

当插入和删除操作发生后，节点左右子树高度差大于 1，不平衡的时候，树需要进行旋转操作。操作分为两种，左旋和右旋。往哪边旋转，根节点就往哪边倒。

👉右旋

这里节点 5 的左树高度是 2，右树高 1，这时候给它插入一个 1，左树高 3，根节点 5 不平衡，进行一次右旋，根节点往右倒，根节点的左子树变成了其原左节点的右子树（LL）。

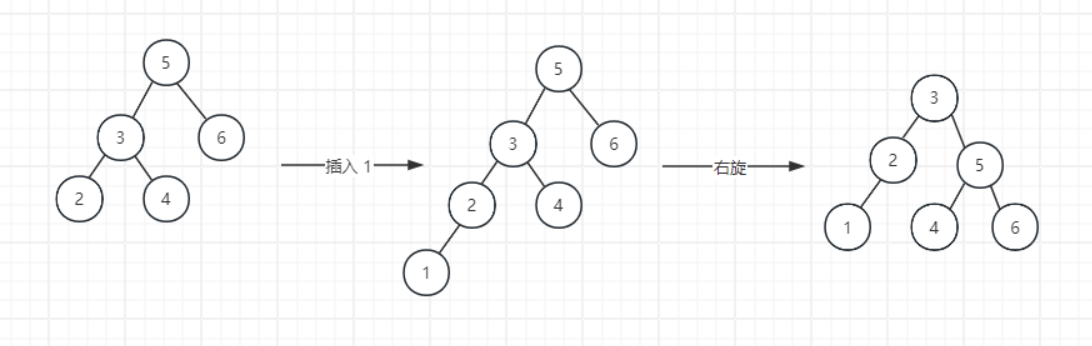
这里把旋转后的子树根节点返回出去，用来给上层的节点调整子树指针。

rust
fn right_rotate(mut node: BoxAVLTreeNode) -> BoxAVLTreeNode {
    let mut child = node.left.unwrap();
    node.left = child.right;
    Self::update(&mut node);
    child.right = Some(node);
    Self::update(&mut child);
    child
}
fn right_rotate_option(node: OptionBoxAVLTreeNode) -> OptionBoxAVLTreeNode {
    match node {
        Some(node) => {
            Some(Self::right_rotate(node))
        },
        None => node
    }
}

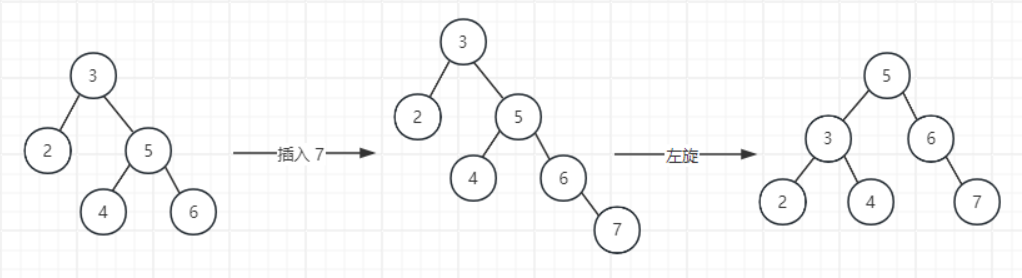
👈左旋

左旋也类似，根节点往左倒，根节点的右子树是原右节点的左子树（RR）：

rust
fn left_rotate(mut node: BoxAVLTreeNode) -> BoxAVLTreeNode {
    let mut child: BoxAVLTreeNode = node.right.unwrap();
    node.right = child.left;
    Self::update(&mut node);
    child.left = Some(node);
    Self::update(&mut child);
    child
}
fn left_rotate_option(node: OptionBoxAVLTreeNode) -> OptionBoxAVLTreeNode {
    match node {
        Some(node) => {
            Some(Self::left_rotate(node))
        },
        None => node
    }
}

💢四种旋转情况

AVL 树不平衡有四种情况，分别是 LL、LR、RR、RL。右旋和左旋的图示分别是 LL、RR 的情况。LL 就是指左节点的左子树高大于等于左节点的右子树高，只需要一次右旋。LR 则是左节点左子树高小于它右子树高，这需要左节点先进行一次左旋，变成 LL 的样子，根节点再进行一次右旋。

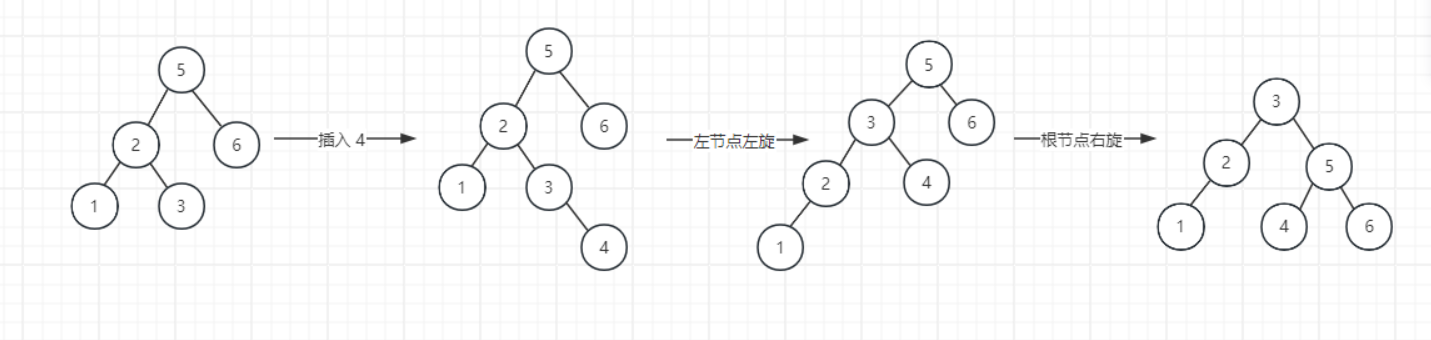
RR 和 RL 则和 LL 和 LR 是对称的，这里就不详述了。来看代码：

rust
fn balance_factor_option(node: &OptionBoxAVLTreeNode) -> i32 {
    match node {
        None => 0,
        Some(node) => {
            Self::balance_factor(node)
        }
    }
}
fn balance_factor(node: &BoxAVLTreeNode) -> i32 {
    Self::height(&node.left) - Self::height(&node.right)
}
fn rotate(node: BoxAVLTreeNode) -> BoxAVLTreeNode {
    let balance_factor = Self::balance_factor(&node);
    if balance_factor > 1 {
        let mut node = node;
        if Self::balance_factor_option(&node.left) >= 0 {
            Self::right_rotate(node)
        } else {
            let left = node.left;
            node.left = Self::left_rotate_option(left);
            Self::right_rotate(node)
        }
    }
    else if balance_factor < -1 {
        let mut node = node;
        if Self::balance_factor_option(&node.right) <= 0 {
            Self::left_rotate(node)
        } else {
            let right = node.right;
            node.right = Self::right_rotate_option(right);
            Self::left_rotate(node)
        }
    } else {
        node
    }
}

🔍搜索

简单地遍历二叉搜索树就可以了。如果查找的key小于当前的就向左查找，大于向右查找。

rust
fn search(&self, key: i32) -> &OptionBoxAVLTreeNode {
    let mut cur = &self.root;
    while let Some(current) = cur {
        match current.key.cmp(&key) {
            Ordering::Less => {
                cur = &current.right;
            }
            Ordering::Greater => {
                cur = &current.left;
            }
            Ordering::Equal => {
                break;
            }
        }
    }
    cur
}

➕插入

插入就是二叉搜索树的插入，再加上平衡树的检查，就不多说了。如果插入的key小于当前的就向左查找，大于向右查找，遍历到空节点就创建一个新节点。如果要插入的key等于当前节点则使当前节点count += 1。

rust
fn insert(&mut self, key: i32) {
    self.root = Self::insert_helper(self.root.take(), key);
}
fn insert_helper(node: OptionBoxAVLTreeNode, key: i32) -> OptionBoxAVLTreeNode {
    match node {
        Some(mut node) => {
            match {
                let node_val = node.key;
                node_val
            }
            .cmp(&key)
            {
                Ordering::Greater => {
                    node.left = Self::insert_helper(node.left, key);
                }
                Ordering::Less => {
                    node.right = Self::insert_helper(node.right, key);
                }
                Ordering::Equal => {
                    node.count += 1;
                }
            }
            Self::update(&mut node);
            Some(Self::rotate(node))
        },
        None => {
            Some(AVLTreeNode::new(key))
        }
    }
}

❌删除

删除也一样遍历二叉搜索树，找到待删除节点时有 4 种情况：

1. 待删除节点count > 1，则count -= 1；
2. 否则如果待删除节点左右有一个为空，则用非空节点代替待删除节点；
3. 如果左右节点都空，直接删除当前待删除节点；
4. 如果左右都不空，则找待删除节点右子树最左节点代替待删除节点。

这里我返回一个布尔值表示待删除节点是否存在。使用了查找节点后继的操作来寻找情况 4 的右子树最左节点。

rust
fn remove(&mut self, val: i32) -> bool {
    let ans = Self::remove_helper(self.root.take(), val, false);
    self.root = ans.0;
    ans.1
}
fn remove_helper(node: OptionBoxAVLTreeNode, key: i32, reomve_node: bool) -> (OptionBoxAVLTreeNode, bool) {
    match node {
        Some(mut node) => {
            let mut match_key = false;
            if key < node.key {
                let ans = Self::remove_helper(node.left, key, reomve_node);
                node.left = ans.0;
                match_key = ans.1
            } else if key > node.key {
                let ans = Self::remove_helper(node.right, key, reomve_node);
                node.right = ans.0;
                match_key = ans.1;
            } else {
                match_key = true;
                if !reomve_node && node.count > 1 {
                    node.count -= 1;
                } else if node.left.is_none() || node.right.is_none() {
                    let child = if node.left.is_some() {
                        node.left
                    } else {
                        node.right
                    };
                    match child {
                        None => {
                            return (None, match_key);
                        }
                        Some(child) => node = child,
                    }
                } else {
                    let right = node.right.take().unwrap();
                    let (next_key, next_count) = Self::next_helper(&right, node.key);
                    node.right = Some(right);
                    let ans = Self::remove_helper(node.right, next_key, true).0;
                    node.right = ans;
                    node.key = next_key;
                    node.count = next_count;
                }
            }
            Self::update(&mut node);
            node = Self::rotate(node);
            (Some(node), match_key)
        }
        None => (None, false),
    }
}
fn next_helper_option(node: &OptionBoxAVLTreeNode, key: i32) -> (i32, i32) {
    match node {
        Some(cur) => {
            Self::next_helper(cur, key)
        },
        None => (i32::MAX, 1)
    }
}
fn next_helper(node: &BoxAVLTreeNode, key: i32) -> (i32, i32) {
    let cur_key = node.key;
    if cur_key <= key {
        Self::next_helper_option(&node.right, key)
    } else {
        let ans = Self::next_helper_option(&node.left, key);
        if cur_key <= ans.0 {
            (cur_key, node.count)
        } else {
            ans
        }
    }
}

🔗查询前驱后继

查找节点前一个值的节点和后一个值的节点，也就是找到小于其的最大值和大于其的最小值，这是一个常见的查询操作。这里的后继查询next_helper，返回了key和count，主要是方便上面的删除操作。在 AVL 树上只需 $O(logn)$ 的时间复杂度。

rust
fn pre(&self, key: i32) -> i32 {
    Self::pre_helper(&self.root, key)
}
fn pre_helper(node: &OptionBoxAVLTreeNode, key: i32) -> i32 {
    match node {
        Some(cur) => {
            let cur_key = cur.key;
            if cur_key >= key {
                Self::pre_helper(&cur.left, key)
            } else {
                cur_key.max(Self::pre_helper(&cur.right, key))
            }
        },
        None => i32::MIN
    }
}
fn next(&self, key: i32) -> i32 {
    Self::next_helper_option(&self.root, key).0
}
fn next_helper_option(node: &OptionBoxAVLTreeNode, key: i32) -> (i32, i32) {
    match node {
        Some(cur) => {
            Self::next_helper(cur, key)
        },
        None => (i32::MAX, 1)
    }
}
fn next_helper(node: &BoxAVLTreeNode, key: i32) -> (i32, i32) {
    let cur_key = node.key;
    if cur_key <= key {
        Self::next_helper_option(&node.right, key)
    } else {
        let ans = Self::next_helper_option(&node.left, key);
        if cur_key <= ans.0 {
            (cur_key, node.count)
        } else {
            ans
        }
    }
}

🏅获取排序和根据排序查询

通过rank函数可以查询到节点排序（从 1 开始）。根据排序查询对应的节点，这也是经典的第 k 大的算法题了，在二叉搜索树上已经排序了，直接找到对应排序的节点即可。在 AVL 树上也只需 $O(logn)$ 的时间复杂度。

rust
fn rank(&self, key: i32) -> i32 {
    Self::rank_helper(&self.root, key) + 1
}
fn rank_helper(node: &OptionBoxAVLTreeNode, key: i32) -> i32 {
    match node {
        Some(cur) => {
            if cur.key >= key {
                Self::rank_helper(&cur.left, key)
            } else {
                Self::size(&cur.left) + cur.count + Self::rank_helper(&cur.right, key)
            }
        },
        None => 0
    }
}
fn index(&self, idx: i32) -> i32 {
    Self::index_helper(&self.root, idx).unwrap()
}
fn index_helper(node: &OptionBoxAVLTreeNode, idx: i32) -> Option<i32> {
    match node {
        Some(cur) => {
            let left = &cur.left;
            let left_size = Self::size(&left);
            let cur_count = cur.count;
            if left_size >= idx {
                let ans = Self::index_helper(&left, idx);
                if !ans.is_none() { ans } else { Some(i32::MIN) }
            } else if left_size + cur_count < idx {
                let right = &cur.right;
                let ans = Self::index_helper(&right, idx - left_size - cur_count);
                if !ans.is_none() { ans } else { Some(i32::MAX) }
            } else {
                Some(cur.key)
            }
        },
        None => None
    }
}

🌈结语

这篇博客用 rust 实现了一个 AVL 树，并且实现了对排序、前驱后继节点查询的操作。

参考：
【算法讲解148【扩展】有序表专题1-AVL树】 https://www.bilibili.com/video/BV1h5yXYJE6t/?share_source=copy_web&vd_source=a06db201a5f7fab5fe54f12bff164f84
【Hello 算法】 https://www.hello-algo.com/chapter_tree/avl_tree/#754-avl